하이 ..
전에 dfs 알고리즘에 대해 글을 올린적이 있다.
https://devkingdom.tistory.com/263?category=956302
DFS (Depth-First Search) 알고리즘 정리
오늘은 알고리즘에서 가장 중요한 개념중에 하나인 DFS에 대해 설명을 드리고자 한다. DFS는 다양한 경우의 수를 구할때 굉장히 많이 쓰이는 알고리즘이나 꼭 익혀두길 권장한다. 일단 코드소스
devkingdom.tistory.com
오늘은 우리가 고등학교 시절 수학시간에 배웠던 순열, 조합 을 dfs 알고리즘을 이용해서 구현해보려고한다.
중복순열
중복순열은 서로 다른 n개 중 r 개를 순서를 고려해서 나열하는 순열을 의미한다. 기로호는 nΠr 로 나타낼 수 있다.
이를 dfs로 각 경우의 수를 print하는 코딩을 하면 아래와 같다.
import java.util.Scanner;
public class PermutationWithRepetition {
static int[] permutation;
static int n,r;
public static void main(String[] args) {
PermutationWithRepetition pwp = new PermutationWithRepetition();
Scanner in = new Scanner(System.in);
n = in.nextInt();
r = in.nextInt();
permutation = new int[r];
pwp.dfs(0);
}
public void dfs(int level) {
if(level == r) {
for(int num : permutation) {
System.out.print(num + " ");
}
System.out.println();
} else {
for(int i=1; i<=n; i++) {
permutation[level] = i;
dfs(level+1);
}
}
}
}만약 n 에 3 ,r 에 2를 넣어주면, 위의 코드는 아래와 같이 동작할 것이다.
그리고 dfs가 어떻게 흘러가는 트리 형태로 그려보면 아래와 같이 그려진다.

잘 이해가 안되시는 분들은 stack 까지 그려놓고 한번 쭉 그려보시길 권장한다.
순열
순열은 서로다른 n개 중 r 개를 골라서 순서를 고려해 나열한 경우의 수를 의미한다. 중복순열과는 다르게 중복은 제거해줘야한다. 기호로는 nPr로 표시한다.
이를 dfs로 각 경우의 수를 print하는 코딩을 하면 아래와 같다.
import java.util.Scanner;
public class Permutation {
static int[] permutation, check, arr;
static int n,r;
public static void main(String args[]) {
Permutation main = new Permutation();
Scanner in = new Scanner(System.in);
n = in.nextInt();
r = in.nextInt();
arr = new int[n];
for(int i=0; i<n; i++) {
arr[i] = in.nextInt();
}
check = new int[n];
permutation = new int[r];
main.dfs(0);
}
public void dfs(int level) {
if (level == r) {
for(int num : permutation) {
System.out.print(num+" ");
}
System.out.println();
} else {
for(int i=0; i<n; i++) {
if (check[i]==0) {
check[i] = 1;
permutation[level] = arr[i];
dfs(level+1);
check[i]=0;
}
}
}
}
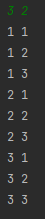
}n 에 3 ,r 에 2를 넣어주고, arr 에 1,2,3을 넣어주면 위의 코드는 아래와 같이 동작할 것이다.

앞에서 중복순열에서 보여줬던 것과 마찬가지로 트리를 그려보면 아래와 같은 형태가 나올 것이다.
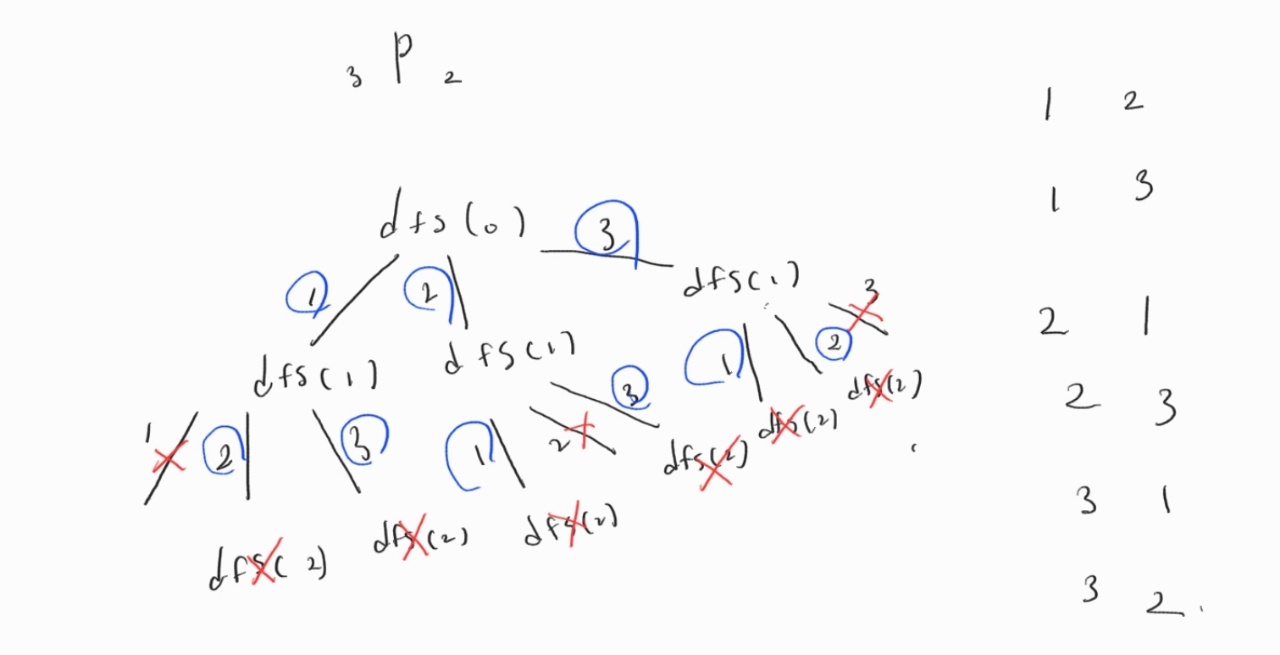
오늘은 간단하게 순열을 구하는 방법을 알아보았다. 스스로 한번 구현해보면 dfs를 조금더 잘 이해할 수 있지 않을까 생각한다 .
'Develop > Algorithm' 카테고리의 다른 글
| 이진탐색 (Binary Search) (0) | 2021.10.03 |
|---|---|
| dfs 를 이용하여 조합 구하기 (0) | 2021.09.12 |
| 백트래킹 (Back Tracking) 알고리즘 이해하기 (0) | 2021.07.29 |
| BFS (Breadth-First Search) 알고리즘 정리 (0) | 2021.07.28 |
| DFS (Depth-First Search) 알고리즘 정리 (0) | 2021.07.28 |




댓글